⚠ EN CONSTRUCCIÓN ⚠
Bienvenidos a la página que contiene el material presentado en el taller de la PyCon España de Granada, el 30 de septiembre de 2022.
El desafío
Un señor de aspecto serio
Supongamos que somos expertos Big Data a nivel mundial, así que parte de nuestro tiempo se dedica a dar charlas en conferencias internacionales para expertos en Big Data. Justo al final de una de un taller de la PyCon un hombre de aspecto serio se nos acerca, nos entrega un sobre con documentación y nos pide que firmemos un recibo.
-¿Sobre qué es la documentación? Preguntamos.
-Es la documentación para participar como perito en un juicio de parte de la acusación. El juicio se celebrará en aproximadamente dos meses. A partir de ahora el contenido de este sobre, su participación como testigo y cualquier indagación que haga queda bajo secreto de sumario. El secretario judicial le contactará cuando se sepa la fecha y hora de su declaración.
El hombre de aspecto serio se va con el mismo aspecto serio sin decir una palabra más, y nos deja plantados en una aula de universidad vacía y silenciosa.
Esa misma noche abrimos el sobre en la habitación de hotel, con el ordenador abierto para ir tomando notas.
El Casino Cansino
La Dirección General de Ordenación del Juego (DGOJ) sospecha que Casinos Cansinos Online, a partir de ahora CCO, está manipulando la generación de números aleatorios para aumentar sus beneficios. Si algo bueno tienen los juegos de azar es que obtener cualquier cantidad, incluida la cantidad de dinero que se embolsa la casa, es un ejercicio de primero de Estadística. La sospecha se centra en el juego de Ruleta Francesa. La casa debería ganar aproximadamente un 2.7% de lo apostado, pero esta cifra es sensiblemente superior. Pero cuando los funcionarios de la DGOJ han revisado los registros históricos de tiradas, no hay indicios que el número 0, que permite a la casa recoger lo apostado por los jugadores, tenga mayor probabilidad de selección que cualquier otro número del 1 al 36.
CCO alega en su defensa que las ganancias por encima de lo esperado siguen estando por debajo del 1% del intervalo de confianza, y que no hay que penalizarles por tener buena suerte, o porque sus clientes sean especialmente torpes jugando a la ruleta. A su vez, los abogados de CCO exigen que si la DGOJ no aporta pruebas concluyentes antes del juicio éste no debe celebrarse, puesto que sólo la apertura de un proceso público dañaría la reputación de CCO de manera irreparable.
Por exigencia del regulador, CCO está obligado a guardar y proporcionar los registros históricos de todas las apuestas y tiradas de cada mesa de ruleta durante los últimos 10 años. Lo que no exige el regulador es que los datos salgan de sus sistemas y que deban proporcionar a los funcionarios o peritos los recursos de cálculo necesarios para investigar cualquier irregularidad.
De este modo, CCO ha proporcionado una máquina virtual con 4 cores, 4 GB de memoria y unos 256 GB de disco conectada a su data lake. No ha proporcionado ningún entorno Hadoop, ningún cluster Spark y mucho menos una suscripción a AWS para levantar los servicios necesarios. Por este motivo los funcionarios de la DG han decidido pedir ayuda a un experto en Big Data.
Los datos
El casino lleva 10 años operando, con unas 100 mesas de Ruleta Francesa realizando tiradas cada minuto ininterrumpidamente. Cada mesa puede tener un máximo de 25 jugadores, límite necesario para que la mesa no se abarrote de apuestas (el regulador obliga a que el juego en los casino online sea lo más parecido posible a un casino real, con lo que es obligatorio que cada jugador vea la apuesta de los otros jugadores). Suponiendo una media de 12 apuestas por tirada (cada jugador puede hacer más de una apuesta), los datos consistirán de
- 10 años
- 0.5M de minutos en un año
- 12 apuestas por minuto
- 100 mesas
Multiplicando las cantidades anteriores tenemos aproximadamente 6G registros, cada uno especificando el instante de tiempo, el jugador, la mesa, la tirada...
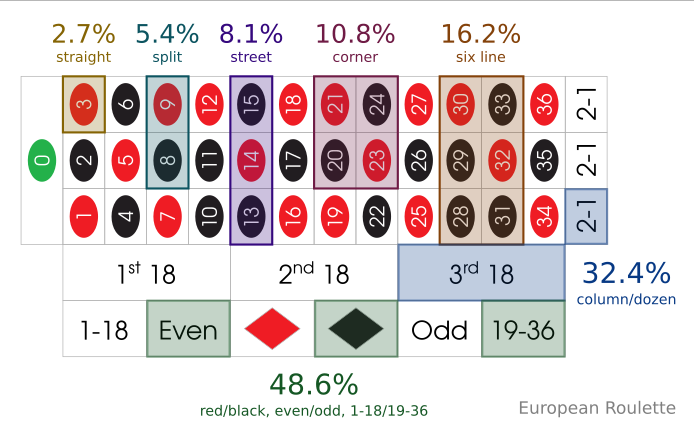
La Ruleta Francesa
La Ruleta Francesa tiene dos componentes principales. El primero es la ruleta, que no es más que un dispositivo que, operado correctamente, elige un número aleatorio entre 0 y 36. El segundo es la mesa, que sirve para que cada jugador realice una apuesta.
Existen 118 apuestas posibles, cada una con un grado distinto de riesgo, y a mayor riesgo, mayor recompensa. La apuesta de mayor riesgo es un número sencillo, con una probabilidad de acierto de 1/37. En el caso de acertar, el jugador recibe ganancias proporcionales al inverso de la probabilidad de acierto sobre 36 opciones. Por ejemplo, si el jugador apuesta al 7 y acierta, la casa le devolverá su apuesta multiplicada por 36. Existen apuestas con una probabilidad mayor, como apostar al color o a la paridad. En ese caso la probabilidad es de 18/37. Si el jugador apuesta al rojo y acierta, entonces sus ganancias serán el doble de lo apostado. Las apuestas compuestas no incluyen nunca el número 0, que es la apuesta de la casa. Cuando la bola de la ruleta cae en el 0, la casa recoge todas las apuestas a excepción de las apuestas simples al 0. Es así como la casa recoge su comisión por operar la ruleta.
Existe otra variante alternativa de ruleta, la americana, donde además del 0 se incluye la casilla 00. Esto implica que la casa tiene casi el doble de comisión. En el caso de estar en Las Vegas, no hay elección poisble: todas las ruletas serán americanas, pero hay que ser un poco obtuso para entrar en un casino online y preferir la ruleta americana a la europea.
La primera pregunta que debemos hacernos qué test estadístico debemos plantear y cuál es el intervalo de confianza que podemos obtener con nuestros datos
¿Cuántos datos necesitamos?
Cualquier proyecto de big data debe empezar por esta pregunta. Somos conscientes que exsiste algo llamado calentamiento global, y gastar julios de energía de manera inútil es lo últio que querríamos.
El test binomial es quizás el test más básico de la estadística frecuentista, y también uno de los más útiles. Supongamos un fenómeno en el que el evento x puede producirse con probabilidad ˋpˋ, y no producirse con probabilidad ˋq=1-pˋ. En el caso de la ruleta, la ocurrencia de la casilla 0 tiene sobre el papel una probabilidad de ˋp_0=1/37ˋ, y el resto de opciones alternativas una probabilidad de ˋq_0=36/37ˋ. El test binomial nos permite calcular con qué certeza nuestros datos validan la hipotesis que la probabilidad de obtener un 0 está por debajo (o por encima) de un valor arbitrario de ˋpˋ.
Supongamos que obtenemos una muestra de 10000 partidas de ruleta en las que el número de ocurrencias del 0 (280) es mayor del esperado (270). Cuál es la probabilidad de que la ruleta esté trucada con el objetivo de obtener un 1% adicional de 0?
>>> from scipy import stats
>>> stats.binomtest(280, 10000, p=1.01*1/37, alternative="greater").pvalue
0.3413962283017562
Este resultado singifica que la hipótesis nula, que la ruleta no está manipulada con un margen de confianza del 1%, tiene una probabilidad de 0.34 de ser verdad. Parece que una muestra de 10000 partidas no es suficiente para argumentar delante de un juez si la ruleta tiene el comportamiento esperado o tiene tendencia a favorecer la banca. ¿Cuántas partidas necesitaremos entonces?
Podemos comprobar de manera aproximada el ancho del intervalo de confianza calculando el test para una ruleta teórica que obtiene exactamente el número esperado de 0 y distintos tamaños de muestra:
ssizes = [int(1E5), int(1E6), int(1E7), int(1E8)]
for ssize in ssizes:
x = np.logspace(-5, -1.3, 30)
y =[stats.binomtest(int(ssize/37), ssize, p=1/37*(1+l), alternative="greater").pvalue for l in x]
plt.plot(x, y)
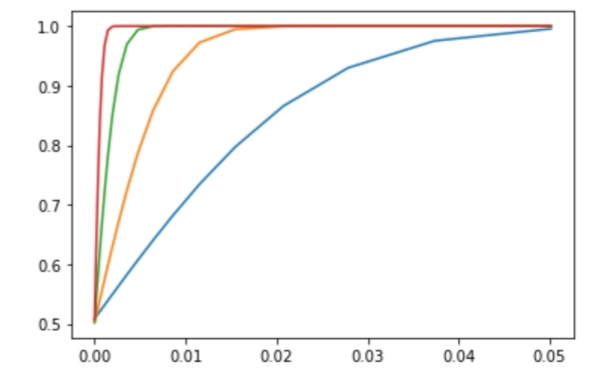
El eje horizontal corresponde a la anchura el intervalo de confianza, y el eje vertical corresponde a la probabilidad que la hipótesis nula se cumpla. Las líneas azul, verde, naranja y roja corresponden a muestras de 100.000, 1.000.000, 10.000.000 y 100.000.000 partidas respectivamente. Para 100.000 partidas obtenemos que sólo podemos afirmar delante de un juez si la ruleta ha sido manipulada para dar un 5% más de ceros. Encontrar pequeñas manipulaciones en la ruleta requiere de más de 10.000.000 de muestras.
Por desgracia tenemos que usar prácticamente todos los datos que tenemos a nuestra disposición.