guillem/PyConES22
guillem/PyConES22
1
0
Fork 0
Code Issues Pull requests Packages Projects Releases Wiki Activity

Update 'HomeES'

Guillem Borrell Nogueras 2022-08-15 15:36:16 +02:00
parent ca8c00f391
commit 8918a6f5ff
1 changed files with 25 additions and 5 deletions
Show stats Download patch file Download diff file Expand all files Collapse all files

28
HomeES.md

@ -19,7 +19,7 @@ Esa misma noche abrimos el sobre en la habitación de hotel, con el ordenador ab
La Dirección General de Ordenación del Juego (DGOJ) sospecha que `Casinos Cansinos Online`, a partir de ahora CCO, está manipulando la generación de números aleatorios para aumentar sus beneficios. Si algo bueno tienen los juegos de azar es que obtener cualquier cantidad, incluida la cantidad de dinero que se embolsa la casa, es un ejercicio de primero de Estadística. La sospecha se centra en el juego de Ruleta Francesa. La casa debería ganar aproximadamente un 2.7% de lo apostado, pero esta cifra es sensiblemente superior. Pero cuando los funcionarios de la DGOJ han revisado los registros históricos de tiradas, no hay indicios que el número 0, que permite a la casa recoger lo apostado por los jugadores, tenga mayor probabilidad de selección que cualquier otro número del 1 al 36.
CCO alega en su defensa que las ganancias por encima de lo esperado siguen estando por debajo del 1% del intervalo de confianza, y que no hay que penalizarles por tener buena suerte, o porque sus clientes sean especialmente torpes jugando a la ruleta.
CCO alega en su defensa que las ganancias por encima de lo esperado siguen estando por debajo del 1% del intervalo de confianza, y que no hay que penalizarles por tener buena suerte, o porque sus clientes sean especialmente torpes jugando a la ruleta. A su vez, los abogados de CCO exigen que si la DGOJ no aporta pruebas concluyentes antes del juicio éste no debe celebrarse, puesto que sólo la apertura de un proceso público dañaría la reputación de CCO de manera irreparable.
Por exigencia del regulador, CCO está obligado a guardar y proporcionar los registros históricos de todas las apuestas y tiradas de cada mesa de ruleta durante los últimos 10 años. Lo que no exige el regulador es que los datos salgan de sus sistemas y que deban proporcionar a los funcionarios o peritos los recursos de cálculo necesarios para investigar cualquier irregularidad.
@ -49,7 +49,9 @@ Existe otra variante alternativa de ruleta, la americana, donde además del 0 se
La primera pregunta que debemos hacernos qué test estadístico debemos plantear y cuál es el intervalo de confianza que podemos obtener con nuestros datos
## El test binomial
## ¿Cuántos datos necesitamos?
Cualquier proyecto de big data debe empezar por esta pregunta. Somos conscientes que exsiste algo llamado calentamiento global, y gastar julios de energía de manera inútil es lo últio que querríamos.
El test binomial es quizás el test más básico de la estadística frecuentista, y también uno de los más útiles. Supongamos un fenómeno en el que el evento *x* puede producirse con probabilidad ˋpˋ, y no producirse con probabilidad ˋq=1-pˋ. En el caso de la ruleta, la ocurrencia de la casilla 0 tiene sobre el papel una probabilidad de ˋp_0=1/37ˋ, y el resto de opciones alternativas una probabilidad de ˋq_0=36/37ˋ. El test binomial nos permite calcular con qué certeza nuestros datos validan la hipotesis que la probabilidad de obtener un 0 está por debajo (o por encima) de un valor arbitrario de ˋpˋ.
@ -57,8 +59,26 @@ El test binomial es quizás el test más básico de la estadística frecuentista
Supongamos que obtenemos una muestra de 10000 partidas de ruleta en las que el número de ocurrencias del 0 (280) es mayor del esperado (270). Cuál es la probabilidad de que la ruleta esté trucada con el objetivo de obtener un 1% adicional de 0?
```python
from scipy import stats
stats.binomtest(280, 10000, p=1.01*1/37, alternative="greater").pvalue
>>> from scipy import stats
>>> stats.binomtest(280, 10000, p=1.01*1/37, alternative="greater").pvalue
0.3413962283017562
```
Este resultado singifica que la hipótesis nula, que la ruleta no está manipulada con un margen de confianza del 1%, tiene una probabilidad de 0.34 de ser verdad. *Parece que una muestra de 10000 partidas no es suficiente para argumentar delante de un juez si la ruleta tiene el comportamiento esperado o tiene tendencia a favorecer la banca*. ¿Cuántas partidas necesitaremos entonces?
Podemos comprobar de manera aproximada el ancho del intervalo de confianza calculando el test para una ruleta teórica que obtiene exactamente el número esperado de 0 y distintos tamaños de muestra:
```python
ssizes = [int(1E5), int(1E6), int(1E7), int(1E8)]
for ssize in ssizes:
x = np.logspace(-5, -1.3, 30)
y =[stats.binomtest(int(ssize/37), ssize, p=1/37*(1+l), alternative="greater").pvalue for l in x]
plt.plot(x, y)
```
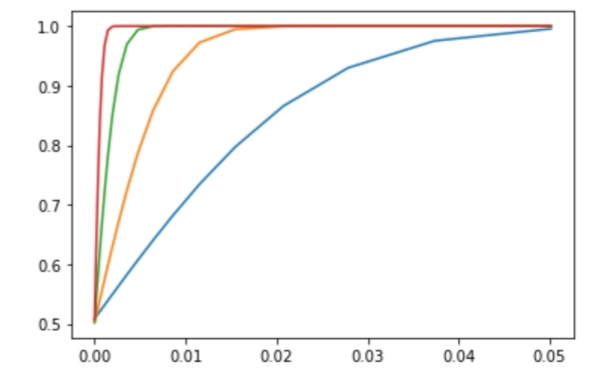
![Convergencia](https://git.guillemborrell.es/guillem/PyConES22/raw/branch/main/doc/fig/convergence.jpg)
El eje horizontal corresponde a la anchura el intervalo de confianza, y el eje vertical corresponde a la probabilidad que la hipótesis nula se cumpla. Las líneas azul, verde, naranja y roja corresponden a muestras de 100.000, 1.000.000, 10.000.000 y 100.000.000 partidas respectivamente. Para 100.000 partidas obtenemos que sólo podemos afirmar delante de un juez si la ruleta ha sido manipulada para dar un 5% más de ceros. Encontrar pequeñas manipulaciones en la ruleta requiere de más de 10.000.000 de muestras.
Por desgracia tenemos que usar prácticamente todos los datos que tenemos a nuestra disposición.